Part of the contents are abstracted from original paper.
This article details elegant design of twin-surface extrapolation from imransai. We will step-by-step derive formula and show why this design works.

Fig. 1, Depth completion task.
Depth completion starts from a sparse set of known depth values and estimates the unknown depths for the remaining image pixels.
Recovering depth discontinuity is that pixels at boundary regions suffer from ambiguity as to whether they belong to a foreground depth or background depth.
–> Propose a multi-hypothesis depth representation that explicitly models both foreground and background depths in the difficult occlusion-boundary regions.
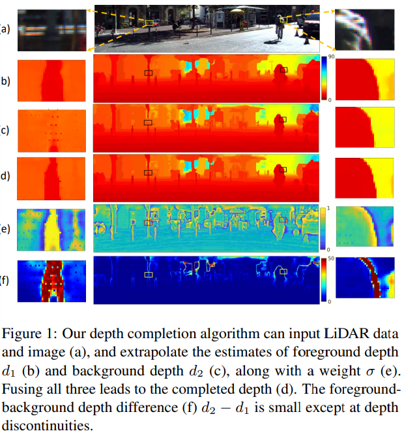
Fig. 2, Illustration of proposed method.
Ambiguities have a significant impact on depth completion, and it is useful to have quantitative way to assess their impact. In this paper, authors proposed using the expected loss to predict and explain the impact of ambguities on trained network.
Simplifying Scene Assumption
We make a further simplifying assumption in our analysis that there are at most binary ambiguities per pixel. A binary ambiguities is described by a pixel having probabilites $p_1$ and $p_2$ of depths $d_1$ and $d_2$ respectively. When $d_1$ < $d_2$ we call $d_1$ the foreground depth and $d_2$ the backfround depth.
To assess the impact of ambiguities on the network, we build a quantitative model. Consider a single pixel whose has a prediction depth $d$, and has a set of ambiguities, $d_i$, each with probability $p_i$. It means that each $d_i$ may has a probability $p_i$ act as ground truth depth. Then, we design the expected loss as a function of depths is:
\[E\{L(d)\}=\sum_i p_i L(d-d_i)\]Since we have simplified assumption, so we get:
\[E\{L(d)\}=p_1 L(d-d_1) + p_2 L(d-d_2)\]Note that expected loss expresses the optimization of training, it is used to predict the behavior of trained network at ambiguities, then justify the design of proposed method. You may also be confused about how to detemine $p_i$, just keep in mind, we will talk about it later.
Loss function is a key component of depth completion. Authors proposed to use two assymetric loss functions to learn foreground and background depth, and to use fusion loss to learn how to select/blend between foreground and background depth.
Foreground and Background Estimators

Fig. 3, Asymmetric Linear Error (ALE) and its twin.
In this paper, authors use a pair of error funtions as shown in Fig.3, which we call the Asymmetric Linear Error ($ALE$), and its twin, the Reflected Asymmetric Linear Error($RALE$), defined as:
\[ALE_{\gamma}=max(-\frac{1}{\gamma} \varepsilon, \gamma \varepsilon)\] \[RALE_{\gamma}=max(\frac{1}{\gamma} \varepsilon, -\gamma \varepsilon)\]Here $\varepsilon$ is the difference between the measurement and the ground truth, $\gamma$ is a parameter, and $max(𝑎,𝑏)$ returns the larger of $𝑎$ and $𝑏$. Note that if $\gamma$ is replaced by $1/\gamma$, both the $ALE$ and $RALE$ are reflected. Thus, without loss of generality, we restrict $\gamma \geq 1$ in this work.
To estimate the foreground depth, authors proposed to minimizing the mean $ALE$ over all pixels to obtain $\hat{d}_1$, the estimated foreground surface. By examing expected $ALE$, we will know what an ideal network will predict.
The full expected $ALE$ loss will be:
\[E\{L(d)\}=E\{ALE_{\gamma}(\varepsilon)\}\] \[=p_1 ALE_{\gamma}(d-d_1) + p_2 ALE_{\gamma}(d-d_2)\] \[=p_1 max(-\frac{1}{\gamma} (d-d_1), \gamma (d-d_1)) + p_2 max(-\frac{1}{\gamma} (d-d_2), \gamma (d-d_2))\]we obtain expected losses at ambiguities $d_1$ and $d_2$:
\[E\{L(d_1)\}=p_1 max(-\frac{1}{\gamma} (d_1-d_1), \gamma (d_1-d_1)) + p_2 max(-\frac{1}{\gamma} (d_1-d_2), \gamma (d_1-d_2))\] \[=p_2 (-\frac{1}{\gamma} (-(d_2-d_1))), \because d_1 < d_2\] \[=p_2 \frac{1}{\gamma} (d_2-d_1)\] \[E\{L(d_2)\}=p_1 max(-\frac{1}{\gamma} (d_2-d_1), \gamma (d_2-d_1)) + p_2 max(-\frac{1}{\gamma} (d_2-d_2), \gamma (d_2-d_2))\] \[=p_1 \gamma (d_2-d_1), \because d_1 < d_2\]To estimate foreground depth, it is straightforward to see that:
\[L(d_1)<L(d_2)\]The equation is satisfied only when:
\[p_2 \frac{1}{\gamma} (d_2-d_1) < p_1 \gamma (d_2-d_1)\] \[\gamma > \sqrt{\frac{p_2}{p_1}} \qquad (Constraint \; 1)\]Fig.4 demonstrates the behavior of foreground depth estimator, we fix $d_1$ and $d_2$ to be $4$ and $8$, respectively. Then dynamically change the ratio of $p_1$ and $p_2$, to see the well-restricted $\gamma$ is needed.
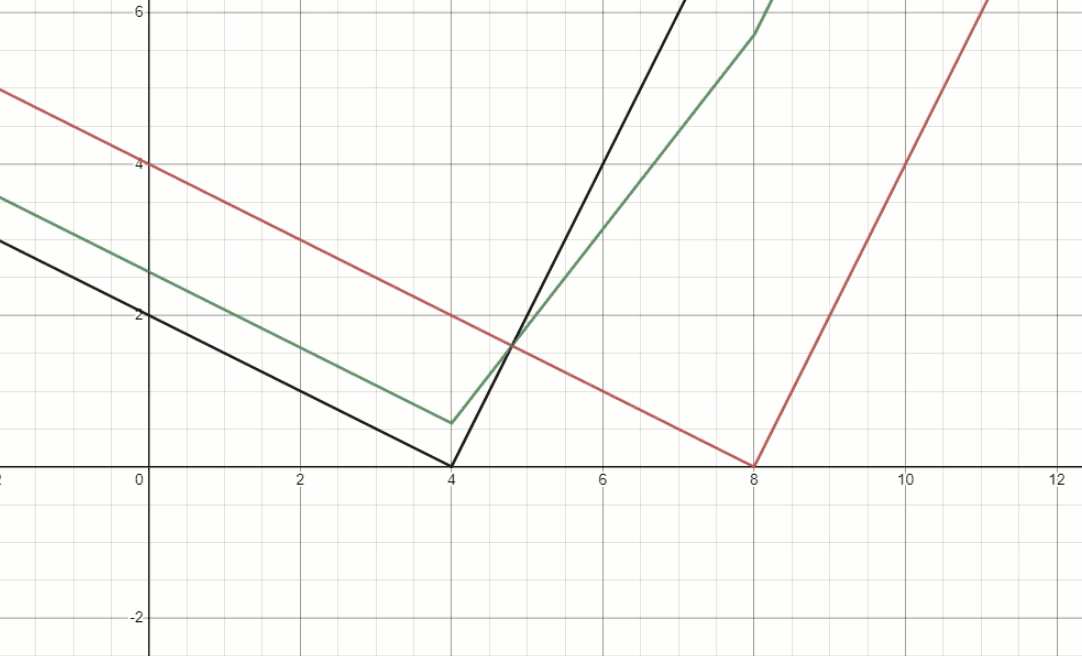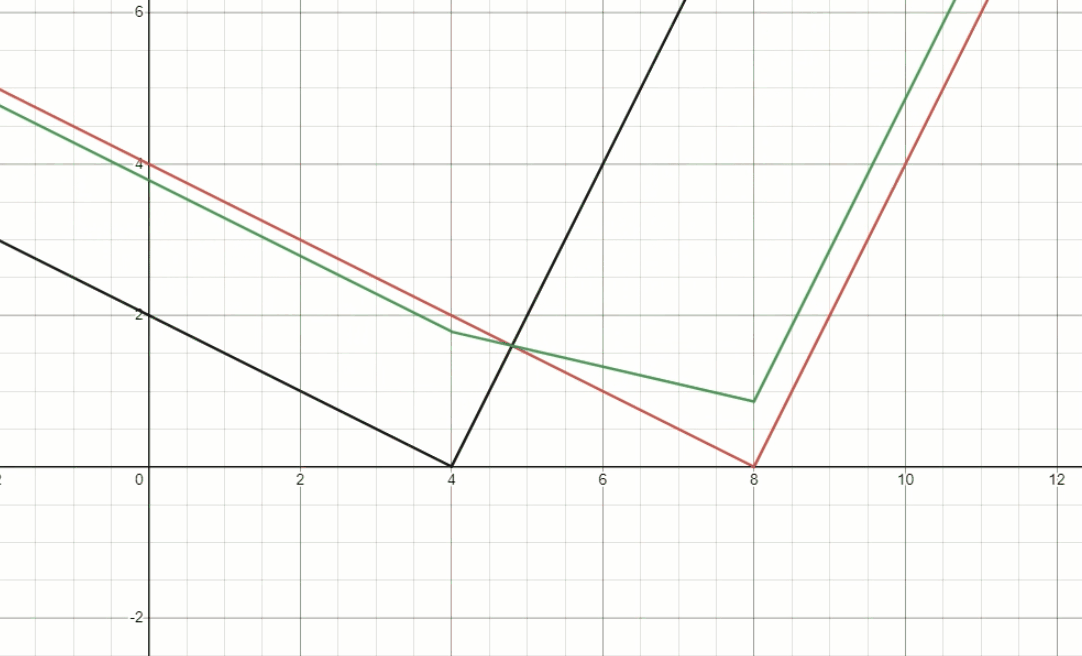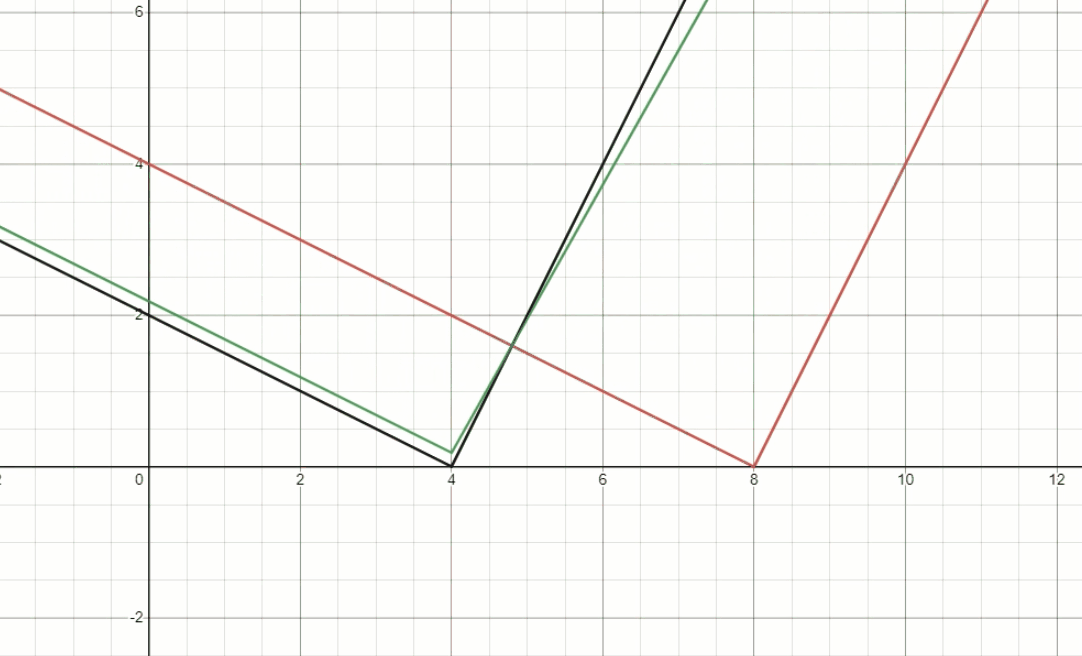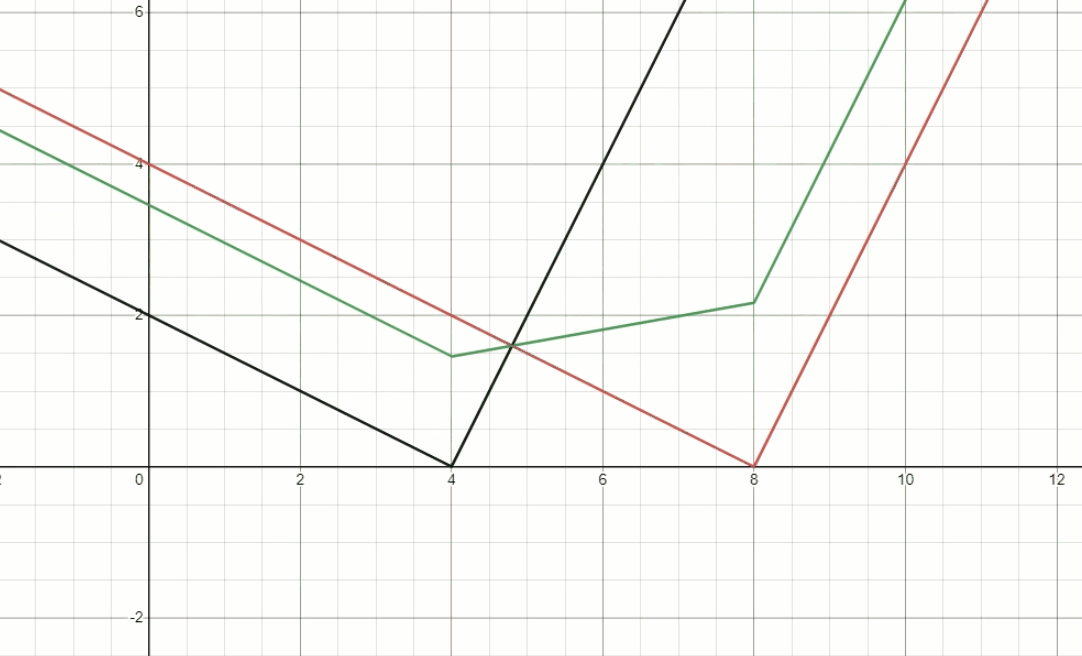
Fig. 4, The behavior of foreground depth estimator.
The same analysis, to estimate the background depth, authors proposed to minimizing the mean $RALE$ over all pixels to obtain $\hat{d}_2$, the estimated background surface. By examing Expected RALE, we get the same constraint on $\gamma$, except that the probability ration ins inverted.
The full expected $RALE$ loss will be:
\[E\{L(d)\}=E\{RALE_{\gamma}(\varepsilon)\}\] \[=p_1 RALE_{\gamma}(d-d_1) + p_2 RALE_{\gamma}(d-d_2)\] \[=p_1 max(\frac{1}{\gamma} (d-d_1), -\gamma (d-d_1)) + p_2 max(\frac{1}{\gamma} (d-d_2), -\gamma (d-d_2))\]we obtain expected losses at ambiguities $d_1$ and $d_2$:
\[E\{L(d_1)\}=p_1 max(\frac{1}{\gamma} (d_1-d_1), -\gamma (d_1-d_1)) + p_2 max(\frac{1}{\gamma} (d_1-d_2), -\gamma (d_1-d_2))\] \[=p_2 \gamma (d_2-d_1), \because d_1 < d_2\] \[E\{L(d_2)\}=p_1 max(\frac{1}{\gamma} (d_2-d_1), -\gamma (d_2-d_1)) + p_2 max(\frac{1}{\gamma} (d_2-d_2), -\gamma (d_2-d_2))\] \[=p_1 \frac{1}{\gamma} (d_2-d_1), \because d_1 < d_2\]To estimate background depth, it is straightforward to see that:
\[L(d_1)>L(d_2)\]The equation is satisfied only when:
\[p_2 \gamma (d_2-d_1) > p_1 \frac{1}{\gamma} (d_2-d_1)\] \[\gamma > \sqrt{\frac{p_1}{p_2}} \qquad (Constraint \; 2)\]Fused Depth Estimator
We desire to have a fused depth predictor, and we know the foreground and background depth estimates provide lower and upper bounds on depth for each pixel. We express the final fused depth estimator $\hat{d}_t$ for the true depth $d_t$ as a weighted combination of the two depths:
\[\hat{d}_t = \sigma \hat{d}_1 + (1-\sigma) \hat{d}_2\]where $\sigma$ is an estimated value between $0$ and $1$. We use a mean absolute error as part of the fusion loss:
\[F(\sigma)=|\hat{d}_t-d_t|=|\sigma \hat{d}_1 + (1-\sigma) \hat{d}_2-d_t|\]To estimate fused depth, we examing the loss below:
\[L(\sigma) = E\{F(\sigma)\} = p|\sigma \hat{d}_1 + (1-\sigma) \hat{d}_2-d_1| + (1-p)|\sigma \hat{d}_1 + (1-\sigma) \hat{d}_2-d_2|\]Here, $p=p_1$, and $p_2=1-p$. This has a minimum at $\sigma=1$ when $𝑝>0.5$ and a minimum at $\sigma=0$ when $𝑝<0.5$, we also draw the hyperplane of $L(\sigma)$ in Fig.5, the optimize direction guides the model predict either foreground depth $d_1$ or background depth $d_2$.
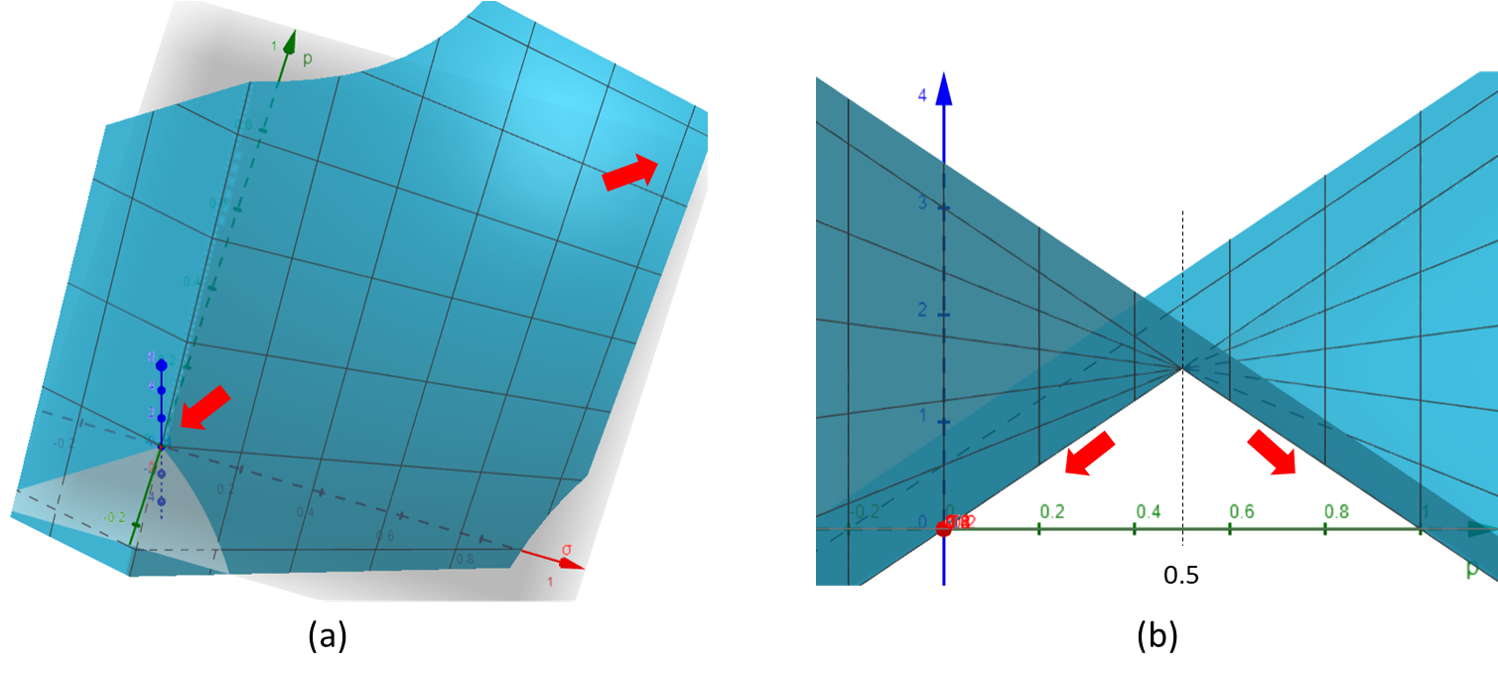
Fig. 5, The hyperplane of $L(\sigma)$.
We have developed three separate loss function whose individual optimazations give us three separate components of a final depth estimate for each pixel. Based on the characterization of our losses, we require a network to produce a 3-channel output. Then for simplicity we combine all loss functions into a single loss:
\[L(c_1, c_2, c_3) = \frac{1}{N} \sum_{j}^{N}(ALE_{\gamma}(c_{1j}-d_1) + RALE_{\gamma}(c_{2j}-d_2) + F(s(c_{3j})))\]Here $𝑐_{𝑖𝑗}$ refers to pixel $j$ of channel $i$, $s()$ is a Sigmoid function, and the mean is taken over all $𝑁$ pixels. We interpret the output of these three channels for a trained network as
\[𝑐_1 \rightarrow \hat{d}_1, 𝑐_2 \rightarrow \hat{d}_2, s(𝑐_3) \rightarrow \sigma\]Now, let’s see what happen here, we force $p_1$ to be $1$, $p_2$ to be $0$, which means the model learn to predict the depth $d$ with only considering foreground depth $d_1$ act as the ground truth depth $d_t$. Given $p_1=1$, $p_2=0$ and $d=\hat{d}_1$:
\[E\{ALE_{\gamma}(\varepsilon)\}=p_1 ALE_{\gamma}(d-d_1) + p_2 ALE_{\gamma}(d-d_2)\] \[=ALE_{\gamma}(\hat{d}_1-d_1)\]By the same token, we have:
\[E\{RALE_{\gamma}(\varepsilon)\}=p_1 RALE_{\gamma}(d-d_1) + p_2 RALE_{\gamma}(d-d_2)\] \[=RALE_{\gamma}(\hat{d}_2-d_2)\]We can further interpret that when the pixel locate at the boundary of foreground and background, $ALE$ tend to guiding the model predict $\hat{d}_1$ to be foreground depth $d_1$. Meanwhile, $RALE$ tend to guiding the model predict $\hat{d}_2$ to be background depth $d_2$. See Fig.6:
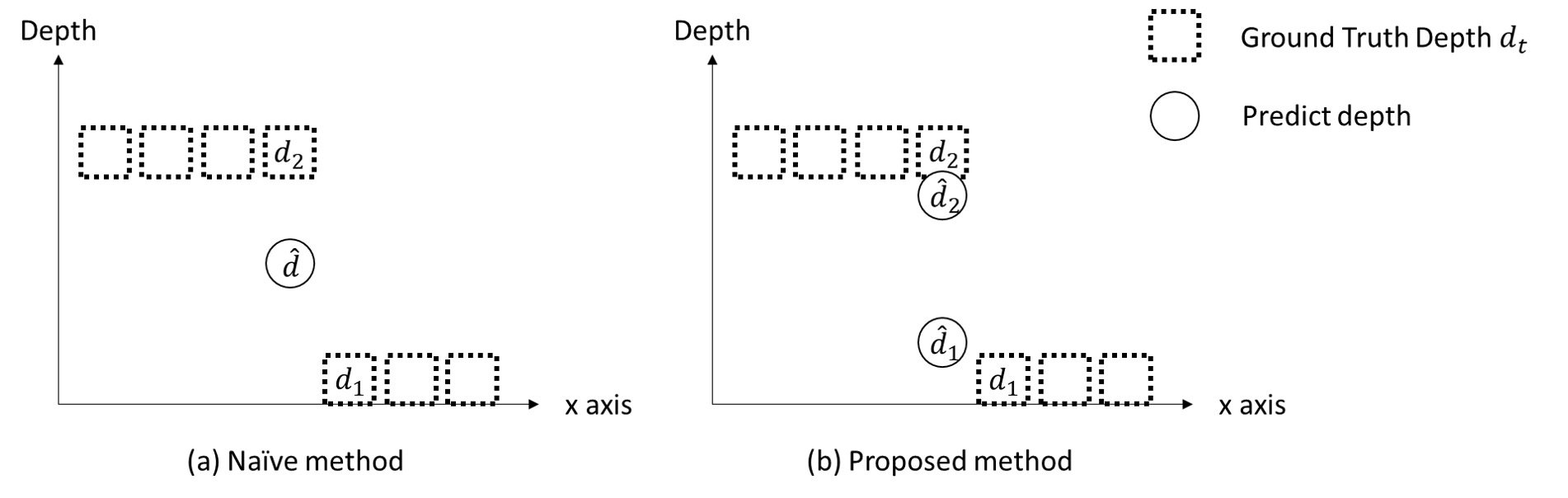
Fig. 6, Visualization of model behavior.
Finally, we have:
\[L(c_1, c_2, c_3) = \frac{1}{N} \sum_{j}^{N}(ALE_{\gamma}(c_{1j}-d_t) + RALE_{\gamma}(c_{2j}-d_t) + F(s(c_{3j})))\]Note that, by doing so, the mentioned $Constraints \;1\; and \;2$ are also satisfied.
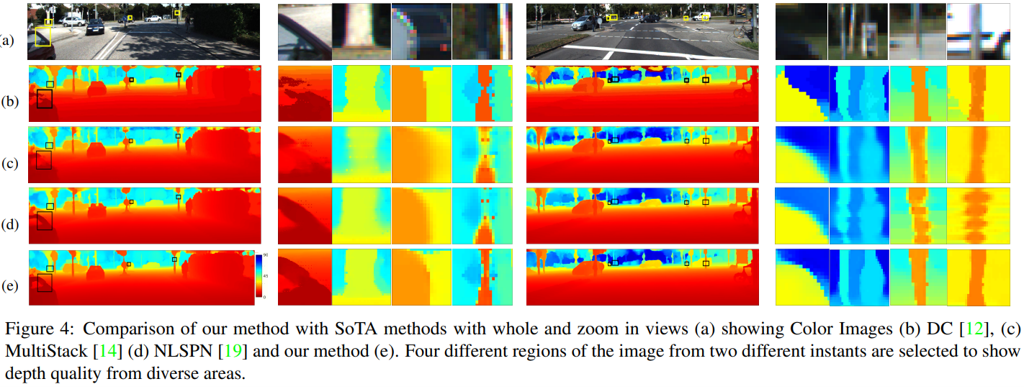
Fig. 7, Comparison of proposed method with SoTA.
[1] Saif Imran, Xiaoming Liu, and Daniel Morris. Depth completion with twin surface extrapolation at occlusion boundaries. In CVPR, pages 2583–2592, 2021.